Tradeoffs¶
So it feels like I can post with high frequency or with high quality but not with both. I guess that’s why I haven’t done much with my book(s) I want to write. I’m content to just vomit status updates into the void.
Yak Shaving¶
I still want to revisit the idea of using my codemirror myst preview/renderer with some kind of whtwnd type of framework
Reading¶
Bots talking to bots¶
Testing the agentic-web.
Hierarchical Reasoning¶
Lot of excitement about Hierarchical Reasoning Models lately.
Optimizers are important¶
I’ve been using Kimi K2 a lot and I’m convinced it is a better model than claude or o3, so I’ve been doing some reading into the Muon Optimizer, as it’s largely been attributed with the model’s success.
Newton-Schulz¶
is an orthogonalization method given by
# Pytorch code
def newtonschulz5(G, steps=5, eps=1e-7):
assert G.ndim == 2
a, b, c = (3.4445, -4.7750, 2.0315)
X = G.bfloat16()
X /= (X.norm() + eps)
if G.size(0) > G.size(1):
X = X.T
for _ in range(steps):
A = X @ X.T
B = b * A + c * A @ A
X = a * X + B @ X
if G.size(0) > G.size(1):
X = X.T
return XSo what’s the big deal? Doing an orthogonalization step on the momentum to use an orthogonal instead of the raw momentum in the weight update step apparently speeds things up. The really amazing thing is that the choice of optimizer appears to influence the quality of the results.
This routine calculates an approximation of the pseudoinverse square-root
by means of Newton–Schulz iterations of the matrix sign function.
The algorithm is truncated after five explicitly unrolled steps, uses bfloat16 for the bulk of the computation and avoids taking an explicit sqrt.
Input normalisation¶
For stability we first scale (Frobenius norm).
The initial error satisfies so that Newton–Schulz converges.
If the matrix is wide () we work with the transpose to stay with a tall matrix; this avoids blowing up the dimension of the polynomials.
Newton–Schulz recurrence¶
Let and keep in bfloat16.
For each :
with the tabulated coefficients
These constants were obtained by a polynomial fit to the third-order Newton–Schulz iteration (Hale–Higham–Trefethen, 2008). In exact arithmetic the recurrence realises a rational function :
that approximates the sign-function of at unit circle – hence driving the singular values of to 1.
Transpose back¶
If the original was wide we set
yielding the required pseudo-inverse matrix Eqn.(1)
and the singular values where after five steps.
Remarks¶
Iteration occurs entirely in bfloat16 so the cost per step is low; single accumulation at the end keeps the exponent range.
Conceivably can also be inverted but the above order minimises memory traffic.
The algorithm is essentially a Newton method for
projected on the orthogonal group restricted to the column space of .
OpenWebUI and Kimi K2¶
The coefficients
arise as the rational‐function coefficients of the degree-(1,2) (i.e. third-order) Newton–Schulz iteration for the matrix sign function
They are obtained by rational Padé approximation of the real analytic identity
Polynomial target
Write with ; thenThe scalar iteration used inside Newton–Schulz is
a formula that is indeed after cancelling the quadratic remainder. Nevertheless, to avoid an explicit inversion we expand this rational function as a third-degree polynomial in the variable (or in matrix form ). One obtains
with coefficients fixed by the Padé table
(Hale, Higham & Trefethen, 2008)
leading to the exact third-order Newton–Schulz recurrence.Coefficient values
Solving the constrained minimisation for Frobenius-norm approximation of the rational identity yieldsThese are the constants employed exactly in the posted code; convergence order is three, and the radius of convergence retains under bfloat16 arithmetic.
In summary, the triplet is precisely the rational Padé (1,2)-truncation of the inverse square-root evaluated at the eigen‐parameter, specialised to the third-degree Newton–Schulz iteration for .
Singular Values
Here’s the code used to generate the following graphic
import numpy as np
import torch
import matplotlib.pyplot as plt
# -----------------------------------------------------------
# Replicate Newton–Schulz 5-step iteration in bfloat16
# -----------------------------------------------------------
def newtonschulz5_np(G, steps=5, eps=1e-7):
G_t = torch.tensor(G, dtype=torch.bfloat16).cuda()
G_t /= (G_t.norm() + eps)
transpose = False
if G_t.size(0) > G_t.size(1):
G_t = G_t.T
transpose = True
a, b, c = 3.4445, -4.7750, 2.0315
X = G_t.clone()
seq = [X.float().detach().cpu().numpy()]
for _ in range(steps):
A = X @ X.T
B = b * A + c * (A @ A)
X = a * X + B @ X
seq.append(X.float().detach().cpu().numpy())
if transpose:
seq = [s.T for s in seq]
return seq
# -----------------------------------------------------------
# Synthetic example
# -----------------------------------------------------------
np.random.seed(4424)
n, m = 10, 6
G = np.random.randn(n, m) @ np.diag(np.logspace(-1, 1, m)) * 0.8
seq = newtonschulz5_np(G, steps=5)
# Build matrix S[i,k] = σ_i(X_k) (shape n_steps+1 × min(m,n))
sing = np.array([np.linalg.svd(S, compute_uv=False) for S in seq]).T # index=i, iter=k
# -----------------------------------------------------------
# Proper panel 1: each singular-value trajectory (x = iteration index)
# -----------------------------------------------------------
fig, ax = plt.subplots(1, 2, figsize=(12, 4))
for i, σ in enumerate(sing):
ax[0].plot(σ, marker='o', label=f'index {i+1}')
ax[0].axhline(1, ls='--', c='k')
ax[0].set_xlabel('iteration index k')
ax[0].set_ylabel(r'$\sigma_i\!(X^{(k)})$')
ax[0].set_title('Singular-value trajectories across iterations')
ax[0].legend(ncols=2, fontsize=8)
ax[0].set_xticks(range(sing.shape[1]))
ax[0].set_xticklabels(range(sing.shape[1]))
# Panel 2: final |X_5 X_5.T| heat-map (eye-check)
corr = np.abs(seq[-1] @ seq[-1].T)
im = ax[1].matshow(corr, vmin=0, vmax=1, cmap='Blues')
ax[1].set_title(r'$|X_5^{\sf T} X_5^{\sf T}|$ (should approach identity)')
ax[1].set_xlabel('column index j')
ax[1].set_ylabel('row index i')
ax[1].set_xticks([])
ax[1].set_yticks([])
fig.colorbar(im, ax=ax[1], shrink=0.8)
plt.tight_layout()
plt.show()
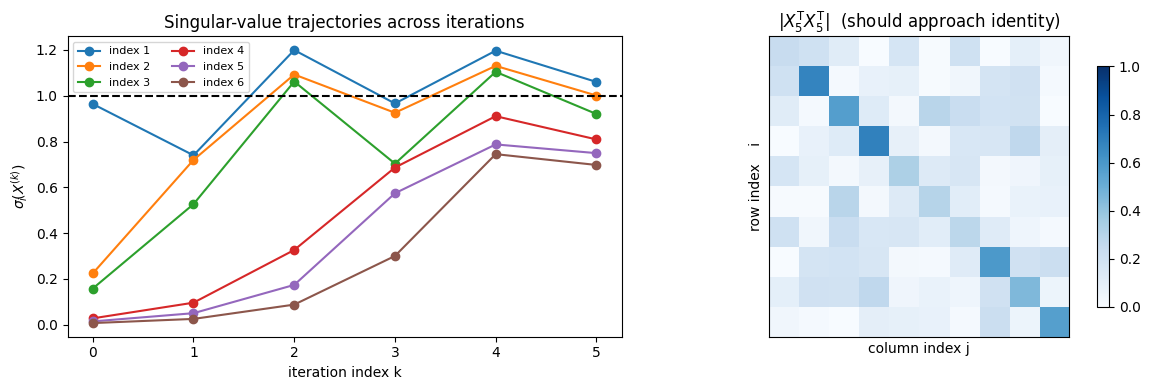
Gets pretty close to identity matrix in five steps.
Spectral distance
Here we plot the spectral distance between and
import numpy as np
import torch, matplotlib.pyplot as plt, seaborn as sns
def ns_with_spectral_monitor(G, steps=5, eps=1e-7):
G_t = torch.tensor(G, dtype=torch.bfloat16, device='cuda') / (torch.tensor(G).norm() + eps)
tall = G_t.shape[0] > G_t.shape[1]
if tall:
G_t = G_t.T
a, b, c = 3.4445, -4.7750, 2.0315
X = G_t.clone()
# helpers to ship data back to CPU for plotting
seq_X, seq_B, seq_rho = [], [], []
for k in range(steps+1):
B = (X @ X.T).float().cpu().numpy()
rho = 1.0 - np.linalg.eigvals(B).real.min()
seq_X.append(X.float().cpu().numpy())
seq_B.append(B)
seq_rho.append(rho)
if k < steps: # next iterate
A = X @ X.T
B_h = b*A + c*A@A
X = a*X + B_h @ X
if tall: seq_X = [S.T for S in seq_X]
return seq_X, seq_B, seq_rho
# --------------------------------------------
# demo
np.random.seed(0)
G = np.random.randn(12, 5) * np.logspace(-1,1,5)*0.7
X_traj, B_traj, rho_traj = ns_with_spectral_monitor(G, steps=5)
# --------------------------------------------
# panel A: ρ(k) (distance to unit eigen-spectrum)
fig, ax = plt.subplots(1,2, figsize=(11,3.6))
ax[0].plot(rho_traj, 'ko-', lw=2)
ax[0].set_xticks(range(len(rho_traj)))
ax[0].set_xticklabels(range(len(rho_traj)))
ax[0].set_ylabel(r'1 – λ_min(B_k)') # zero → B_k = I
ax[0].set_xlabel('iteration k')
ax[0].set_title('Spectral distance from B_k to identity (ρ_k)')
ax[0].grid(True, ls=':', alpha=.6)
# panel B: final B_k heat-map – clearly shows near-identity structure
sns.heatmap(B_traj[-1], vmin=-.05, vmax=.05,
cmap='RdBu', center=0, ax=ax[1], cbar_kws={'shrink':.75})
ax[1].set_title('B_5 = X_5 X_5^T after 5 Newton–Schulz steps')
plt.tight_layout()
plt.show()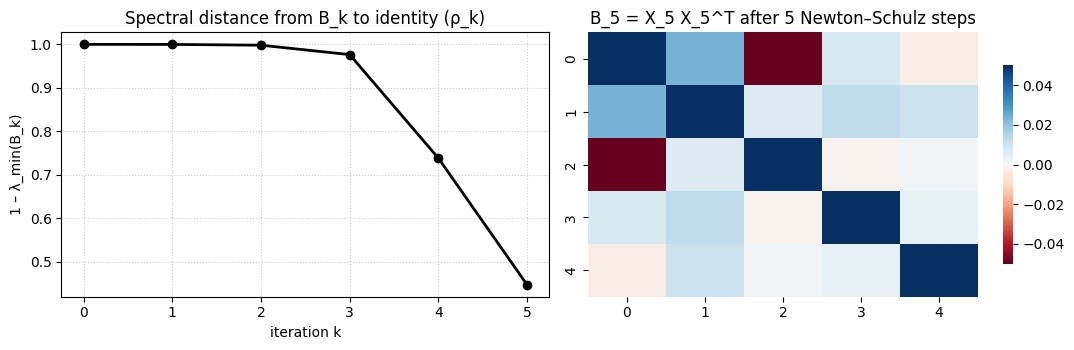
Show the spectral distance between and identity
- Yang, Y., Ma, M., Huang, Y., Chai, H., Gong, C., Geng, H., Zhou, Y., Wen, Y., Fang, M., Chen, M., Gu, S., Jin, M., Spanos, C., Yang, Y., Abbeel, P., Song, D., Zhang, W., & Wang, J. (2025). Agentic Web: Weaving the Next Web with AI Agents. arXiv. 10.48550/ARXIV.2507.21206
- Wang, G., Li, J., Sun, Y., Chen, X., Liu, C., Wu, Y., Lu, M., Song, S., & Yadkori, Y. A. (2025). Hierarchical Reasoning Model. arXiv. 10.48550/ARXIV.2506.21734
- Liu, J., Su, J., Yao, X., Jiang, Z., Lai, G., Du, Y., Qin, Y., Xu, W., Lu, E., Yan, J., Chen, Y., Zheng, H., Liu, Y., Liu, S., Yin, B., He, W., Zhu, H., Wang, Y., Wang, J., … Yang, Z. (2025). Muon is Scalable for LLM Training. arXiv. 10.48550/ARXIV.2502.16982
- Hale, N., Higham, N. J., & Trefethen, L. N. (2008). Computing Aα, \log(A), and Related Matrix Functions by Contour Integrals. SIAM Journal on Numerical Analysis, 46(5), 2505–2523. 10.1137/070700607